We have explored Prime Numbers and Modular Arithmetic in previous articles. Now, we are ready to combine them to build the actual engine of key exchange.
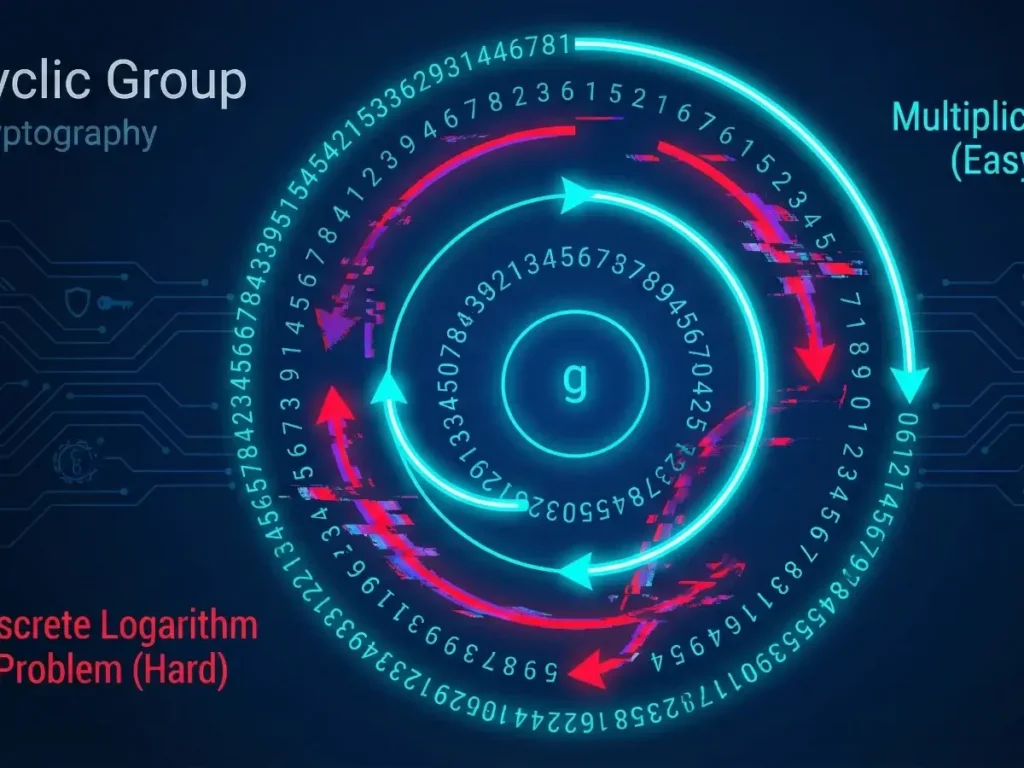
Most modern cryptography (like Diffie-Hellman and ECC) relies on a simple concept: it is easy to mix paint, but impossible to un-mix it. In mathematics, this “mixing” happens inside structures called Cyclic Groups, using a tool called a Generator. The inability to “un-mix” is known as the Discrete Logarithm Problem.
This article explains these three concepts as one cohesive system that secures the internet.
1. What is a Cyclic Group?
In cryptography, we don’t use all numbers. We use a finite set of integers modulo a prime number p. We call this set a “group.”
A group is Cyclic if you can generate every element in the set by taking a single element (let’s call it g) and multiplying it by itself repeatedly.
The “Generator” (g)
The element g is called a Generator (or primitive root). It is the “seed” that grows the entire group.
Example: Modulo 7
Let’s work with the prime p = 7. The available numbers are {1, 2, 3, 4, 5, 6}.
Let’s test if 3 is a generator.
Step 1: Powers of 3
$$ 3^1 \equiv 3 \pmod 7 $$
$$ 3^2 = 9 \equiv 2 \pmod 7 $$
$$ 3^3 = 27 \equiv 6 \pmod 7 $$
$$ 3^4 = 81 \equiv 4 \pmod 7 $$
$$ 3^5 = 243 \equiv 5 \pmod 7 $$
$$ 3^6 = 729 \equiv 1 \pmod 7 $$
Result:
The outputs are {3, 2, 6, 4, 5, 1}.
Notice that we generated every single number from 1 to 6, just in a scrambled order. This means 3 is a generator, and this group is cyclic.
2. The Discrete Logarithm Problem (DLP)
This is where the security comes from. Let’s look at the equation from the example above:
$$ 3^x \equiv 6 \pmod 7 $$
If I give you x = 3, it is easy to calculate that the result is 6. This is called Modular Exponentiation.
But if I reverse it?
“I have a generator 3 and a result 6. What was the exponent x?”
In standard arithmetic, we solve this with logarithms: \( \log_3(6) \). But in Modular Arithmetic, the numbers bounce around randomly. There is no simple pattern (like a curve) to follow.
The Formal Definition
Given a generator g, a prime modulus p, and a result h, find the integer x such that:
$$ g^x \equiv h \pmod p $$
Finding x is the Discrete Logarithm Problem. For small numbers (like 7), it’s easy. For 2048-bit numbers, it is computationally impossible for all the supercomputers on Earth combined.
3. Real World Application: Diffie-Hellman
How do we use Discrete Logarithm and Cyclic Groups to share a password over the internet without anyone seeing it? This is the Diffie-Hellman Key Exchange.
Imagine Alice and Bob want to share a secret key.
1. Public Setup
They agree on a large prime p and a generator g. Everyone knows these.
2. Private Secrets
Alice picks a secret number a.
Bob picks a secret number b.
3. The Mix (One-Way)
Alice calculates A and sends it to Bob:
$$ A = g^a \pmod p $$
Bob calculates B and sends it to Alice:
$$ B = g^b \pmod p $$
(Note: An attacker sees A and B, but cannot find a or b because of the Discrete Logarithm Problem).
4. The Shared Secret
Alice takes Bob’s public B and raises it to her secret a:
$$ s = B^a = (g^b)^a = g^{ba} $$
Bob takes Alice’s public A and raises it to his secret b:
$$ s = A^b = (g^a)^b = g^{ab} $$
Result:
They both have the same number s ($g^{ab}$), but they never sent it over the network.
4. Python Implementation
Here is a script that finds a generator and demonstrates the difficulty of the discrete log (brute force).
def power(a, b, m):
res = 1
a %= m
while b > 0:
if b % 2 == 1:
res = (res * a) % m
a = (a * a) % m
b //= 2
return res
def discrete_log_bruteforce(g, h, p):
# Finds x such that g^x = h (mod p)
# WARNING: Only works for small numbers!
for x in range(p):
if power(g, x, p) == h:
return x
return -1
# Example
p = 17
g = 3
target = 13
x = discrete_log_bruteforce(g, target, p)
print(f"Discrete Log: 3^{x} = {target} (mod {p})")5. Practice Problems
Test your understanding of Discrete Logarithm and Cyclic Groups.
Problem 1: Is 2 a generator of mod 5?
Set: {1, 2, 3, 4}
$$ 2^1 = 2 $$
$$ 2^2 = 4 $$
$$ 2^3 = 8 \equiv 3 $$
$$ 2^4 = 16 \equiv 1 $$
Result: {2, 4, 3, 1}. Yes, it generated all elements.
Problem 2: Simple Discrete Log
Solve for x: $$ 3^x \equiv 4 \pmod 7 $$
Refer to the table in Section 1.
Answer: x = 4.
Conclusion
The beauty of the Discrete Logarithm and Cyclic Groups lies in their asymmetry. It is a mathematical “trapdoor” that is easy to fall through (exponentiation) but incredibly hard to climb back up (logarithm). This asymmetry is the shield that protects your messages in the digital world.