In the fast-paced world of modern computing, algorithms often become obsolete within a few years. However, one algorithm has stood the test of time for over 2,300 years. If you want the Euclidean algorithm explained simply, you are looking at what many consider the “granddaddy” of all algorithms.
First described by the Greek mathematician Euclid around 300 BC, this method is still the most efficient way to compute the Greatest Common Divisor (GCD) of two numbers.
What is the Greatest Common Divisor (GCD)?
Before we dive into the algorithm, let’s refresh the concept. The Greatest Common Divisor (often called the Greatest Common Factor) of two integers is the largest number that divides both of them without leaving a remainder.
Example:
Let’s look at the numbers 12 and 18.
- Divisors of 12: 1, 2, 3, 4, 6, 12
- Divisors of 18: 1, 2, 3, 6, 9, 18
The largest number appearing in both lists is 6. Therefore, $\gcd(12, 18) = 6$.
Why the “School Method” Fails
In school, you might have learned to find the GCD by listing factors or using prime factorization (breaking numbers down into primes).
$$1200 = 2^4 \times 3 \times 5^2$$
As we discussed in our previous article on Prime Numbers Explained, factoring large numbers is incredibly difficult for computers. If you tried to find the GCD of two 100-digit numbers using factorization, your computer would crash long before it finished.
This is where Euclid saves the day.
How the Euclidean Algorithm Works
Euclid realized a fundamental truth about numbers: The GCD of two numbers also divides their difference.
Mathematically, this leads to a powerful reduction property. If we have two numbers, $A$ and $B$ (where $A > B$), then:
$$\gcd(A, B) = \gcd(B, A \pmod B)$$
Here, $A \pmod B$ represents the remainder when $A$ is divided by $B$. This allows us to rapidly shrink the numbers until we reach the answer.
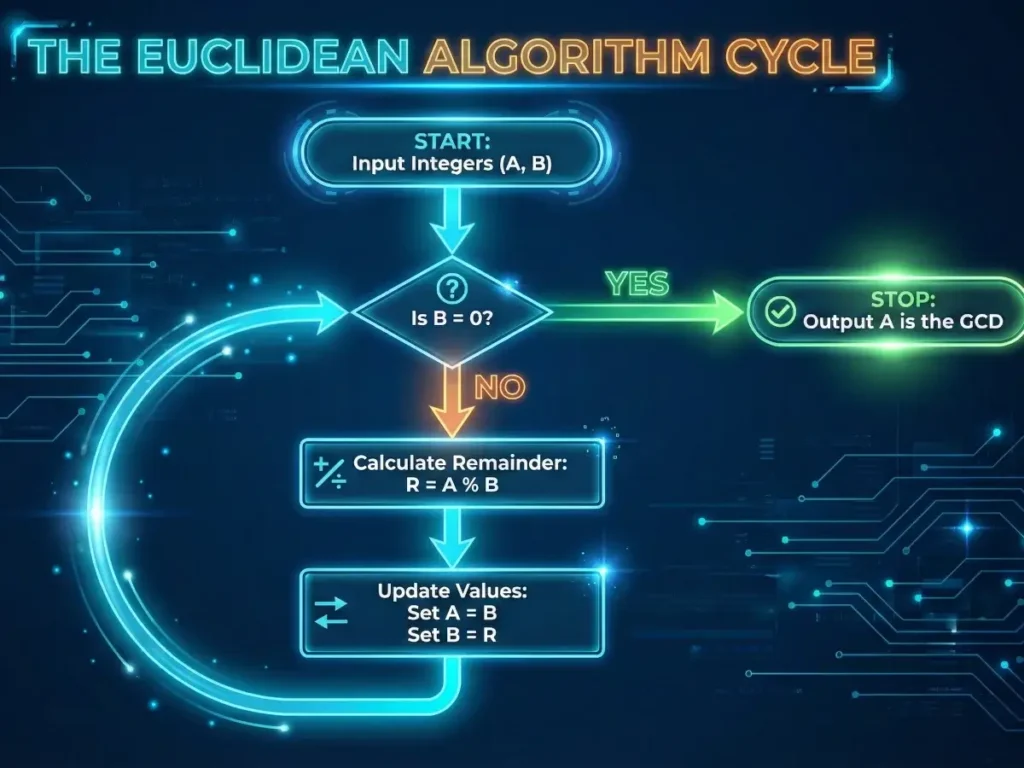
The Step-by-Step Process
- Divide the larger number by the smaller number.
- Take the remainder.
- Make the previous smaller number the new “large” number, and the remainder the new “small” number.
- Repeat until the remainder is 0.
- The last non-zero divisor is the GCD.
A Real-World Example
Let’s calculate the GCD of 270 and 192.
Step 1: Divide 270 by 192.
$$270 = 1 \times 192 + \mathbf{78}$$
(Remainder is 78)
Step 2: Now divide 192 by 78.
$$192 = 2 \times 78 + \mathbf{36}$$
(Remainder is 36)
Step 3: Now divide 78 by 36.
$$78 = 2 \times 36 + \mathbf{6}$$
(Remainder is 6)
Step 4: Now divide 36 by 6.
$$36 = 6 \times 6 + \mathbf{0}$$
(Remainder is 0)
Since the remainder is 0, we stop. The last divisor used was 6.
Therefore, $\gcd(270, 192) = 6$.
Why Is This Useful?
You might wonder why a lawyer or a web developer needs to know 2000-year-old math.
- Cryptography: The Euclidean Algorithm (specifically its “Extended” version) is essential for the RSA encryption that secures the internet. It helps generate the keys used to lock your data.
- Efficiency: While factorization takes exponentially longer as numbers grow, Euclid’s method is incredibly fast. It has logarithmic time complexity, denoted as $O(\log(\min(a, b)))$.
- Design & Grids: In web design, calculating aspect ratios or fitting tiles perfectly into a rectangular space often requires GCD calculations.
Coding the Algorithm (Python)
For those interested in the technical implementation, here is how you would write this in Python. It is elegantly simple:
def gcd(a, b):
while b:
a, b = b, a % b
return a
print(gcd(270, 192)) # Output: 6The Euclidean algorithm proves that the best solutions don’t always require modern technology. By using the simple property of remainders, we can solve complex problems efficiently. Whether you are simplifying fractions or encrypting sensitive data, Euclid’s ghost is still working in the background.
To learn more about the foundational blocks of these numbers, check out our guide on Prime Numbers or explore how these concepts apply to modern Online Security.
